Inequalities Exercise

Assalam'mualaikum and hi again dear bloggers! 

This post will be the simple exercise consisting of the previous post which is inequalities.

1. Solve the inequality z + 5 ≥ 3 and represent its solutions using a number line. 
2. Solve the inequality 4(x – 1) < 3(x + 1) and represent its solutions using a number line. 
3. Graph the following inequality:

1) y  x + 3

2) y > 2x - 1

3) 2y  4x + 6

4) 2x + y > 4

Lastly, 

Which inequality is represented by the graph below?
	Choose:

1. Solve:   3x - 7 < 2
2. Solve:    2x - 5 > x - 2
3.  Solve:    2 - 5x > 3x - 14
4. Solve:   2(y + 1)  y - 4

Graphing Quadratic Inequalities

Here is a video on how to solve a quadratic inequalities on a graph.

"SUCCESS DOESN'T COME 
TO YOU,
YOU GO TO IT."

-MARVA COLLINS-

Before you do so, PLEASE..... do not check for the answer yet if you haven't answered the question yourself. XD 

This is the link to check for the answers: 

http://www.shmoop.com/equations-inequalities/solving-inequalities-exercises.html

http://www.regentsprep.org/regents/math/algebra/ae85/PracGr.htm

Inequalities (Part 4)

Graphing Linear Inequalities

This is a graph of a linear inequality:

The inequality y ≤ x + 2

You can see the y = x + 2 line, and the shaded area is where y is less than or equal to x + 2

Linear Inequality

A Linear Inequality is like a Linear Equation (such as y = 2x+1) ...

... but it will have an Inequality like <, >, ≤, or ≥ instead of an =.

How to Graph a Linear Inequality

First, graph the "equals" line, then shade in the correct area.

There are three steps:

• Rearrange the equation so "y" is on the left and everything else on the right.
• Plot the "y=" line (make it a solid line for y≤ or y≥, and a dashed line for y<or y>)
• Shade above the line for a "greater than" (y> or y≥)
  or below the line for a "less than" (y< or y≤).

Let us try some examples:

Example: y≤2x-1

1. The inequality already has "y" on the left and everything else on the right, so no need to rearrange

2. Plot y=2x-1 (as a solid line because y≤ includes equal to)

3. Shade the area below (because y is less than or equal to)

Example: 2y − x ≤ 6

1. We will need to rearrange this one so "y" is on its own on the left:

Start with: 2y − x ≤ 6

Add x to both sides: 2y ≤ x + 6

Divide all by 2: y ≤ x/2 + 3

2. Now plot y = x/2 + 3 (as a solid line because y≤ includes equal to)

3. Shade the area below (because y is less than or equal to)

Example: y/2 + 2 > x

1. We will need to rearrange this one so "y" is on its own on the left:

Start with: y/2 + 2 > x

Subtract 2 from both sides: y/2 > x − 2

Multiply all by 2: y > 2x − 4

2. Now plot y = 2x − 4 (as a dashed line because y> does not include equals to)

3. Shade the area above (because y is greater than)

The dashed line shows that the inequality does not include the line y=2x-4.

Two Special Cases

You could also have a horizontal or vertical line:

This shows where y is less than 4 (from, but not including, the line y=4 on down) Notice that we have a dashed line to show that it does not include where y=4 This one doesn't even have y in it! It has the line x=1, and is shaded for all values of x greater than (or equal to) 1 Here is 3 videos to understand more about the linear inequalities graphing ^_^

Inequalities (Part 3)

Solving Inequalities

Sometimes we need to solve Inequalities like these:

Symbol	Words	Example
>	greater than	x + 3 > 2
<	less than	7x < 28
≥	greater than or equal to	5 ≥ x - 1
≤	less than or equal to	2y + 1 ≤ 7

Solving

Our aim is to have x (or whatever the variable is) on its own on the left of the inequality sign:

Something like:		x < 5
or:		y ≥ 11

We call that "solved".

How to Solve

Solving inequalities is very like solving equations ... we do most of the same things ...

... but we must also pay attention to the direction of the inequality.

Direction: Which way the arrow "points"

Some things we do will change the direction!

< would become >

> would become <

≤ would become ≥

≥ would become ≤

Safe Things To Do

These are things we can do without affecting the direction of the inequality:

Add (or subtract) a number from both sides
Multiply (or divide) both sides by a positive number
Simplify a side

Example: 3x < 7+3

We can simplify 7+3 without affecting the inequality:

3x < 10

But these things will change the direction of the inequality ("<" becomes ">" for example):

Multiply (or divide) both sides by a negative number
Swapping left and right hand sides

Example: 2y+7 < 12

When we swap the left and right hand sides, we must also change the direction of the inequality:

12 > 2y+7

Here are the details:

Adding or Subtracting a Value

We can often solve inequalities by adding (or subtracting) a number from both sides (just as inIntroduction to Algebra), like this:

Solve: x + 3 < 7

If we subtract 3 from both sides, we get:

x + 3 - 3 < 7 - 3    

x < 4

And that is our solution: x < 4

In other words, x can be any value less than 4.

What did we do?

We went from this: To this:				x+3 < 7 x < 4

And that works well for adding and subtracting, because if we add (or subtract) the same amount from both sides, it does not affect the inequality

Example: Alex has more coins than Billy. If both Alex and Billy get three more coins each, Alex will still have more coins than Billy.

What If I Solve It, But "x" Is On The Right?

No matter, just swap sides, but reverse the sign so it still "points at" the correct value!

Example: 12 < x + 5

If we subtract 5 from both sides, we get:

12 - 5 < x + 5 - 5    

7 < x

That is a solution!

But it is normal to put "x" on the left hand side ...

... so let us flip sides (and the inequality sign!):

x > 7

Do you see how the inequality sign still "points at" the smaller value (7) ?

And that is our solution: x > 7

Note: "x" can be on the right, but people usually like to see it on the left hand side.

Multiplying or Dividing by a Value

Another thing we do is multiply or divide both sides by a value (just as in Algebra - Multiplying).

But we need to be a bit more careful (as you will see).

Positive Values

Everything is fine if we want to multiply or divide by a positive number:

Solve: 3y < 15

If we divide both sides by 3 we get:

3y/3 < 15/3

y < 5

And that is our solution: y < 5

Negative Values

When we multiply or divide by a negative number  we must reverse the inequality.

Why?

Well, just look at the number line!

For example, from 3 to 7 is an increase,
but from -3 to -7 is a decrease.

-7 < -3	7 > 3

See how the inequality sign reverses (from < to >) ?

Let us try an example:

Solve: -2y < -8

Let us divide both sides by -2 ... and reverse the inequality!

-2y < -8

-2y/-2 > -8/-2

y > 4

And that is the correct solution: y > 4

(Note that I reversed the inequality on the same line I divided by the negative number.)

So, just remember:

When multiplying or dividing by a negative number, reverse the inequality

Multiplying or Dividing by Variables

Here is another (tricky!) example:

Solve: bx < 3b

It seems easy just to divide both sides by b, which would give us:

x < 3

... but wait ... if b is negative we need to reverse the inequality like this:

x > 3

But we don't know if b is positive or negative, so we can't answer this one!

To help you understand, imagine replacing b with 1 or -1 in that example:

• if b is 1, then the answer is simply x < 3
• but if b is -1, then we would be solving -x < -3, and the answer would be x > 3

So:

Do not try dividing by a variable to solve an inequality (unless you know the variable is always positive, or always negative).

A Bigger Example

Solve: (x-3)/2 < -5

First, let us clear out the "/2" by multiplying both sides by 2.

Because we are multiplying by a positive number, the inequalities will not change.

(x-3)/2 ×2 < -5 ×2  

(x-3) < -10

Now add 3 to both sides:

x-3 + 3 < -10 + 3    

x < -7

And that is our solution: x < -7

Two Inequalities At Once!

How do we solve something with two inequalities at once?

Solve:

-2 < (6-2x)/3 < 4

First, let us clear out the "/3" by multiplying each part by 3:

Because we are multiplying by a positive number, the inequalities will not change.

-6 < 6-2x < 12

Now subtract 6 from each part:

-12 < -2x < 6

Now multiply each part by -(1/2).

Because we are multiplying by a negative number, the inequalities change direction.

6 > x > -3

And that is the solution!

But to be neat it is better to have the smaller number on the left, larger on the right. So let us swap them over (and make sure the inequalities point correctly):

-3 < x < 6

Summary

• Many simple inequalities can be solved by adding, subtracting, multiplying or dividing both sides until you are left with the variable on its own.
• But these things will change direction of the inequality:
• Multiplying or dividing both sides by a negative number
• Swapping left and right hand sides
• Don't multiply or divide by a variable (unless you know it is always positive or always negative)

Inequalities (Part 2)

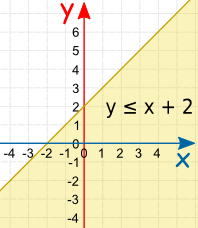
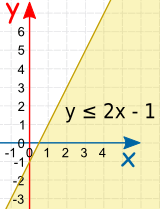
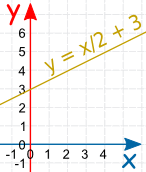
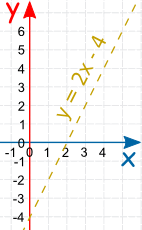
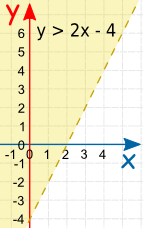
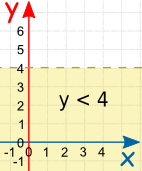
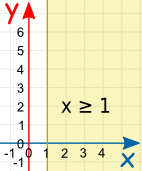
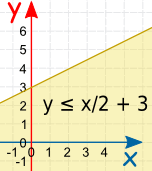Equal, Greater or Less Than

As well as the familiar equals sign (=) it is also very useful to show if something is not equal to (≠) greater than (>) or less than (<)

These are the important signs to know:

=	When two values are equal we use the "equals" sign	example: 2+2 = 4
≠	When two values are definitely not equal we use the "not equal to" sign	example: 2+2 ≠ 9
<	When one value is smaller than another we use a "less than" sign	example: 3 < 5
>	When one value is bigger than another we use a "greater than" sign	example: 9 > 6

Less Than and Greater Than

The "less than" sign and the "greater than" sign look like a "V" on its side, don't they?

To remember which way around the "<" and ">" signs go, just remember:

• BIG > small
• small < BIG

The "small" end always points to the smaller number, like this:

Greater Than Symbol: BIG > small

Example:

10 > 5

"10 is greater than 5"

Or the other way around:

5 < 10

"5 is less than 10"

Do you see how the symbol "points at" the smaller value?

... Or Equal To ...

Sometimes we know a value is smaller, but may also be equal to!

Example, a jug can hold up to 4 cups of water.

So how much water is in it?

It could be 4 cups or it could be less than 4 cups: So until we measure it, all we can say is "less than or equal to" 4 cups.

To show this, we add an extra line at the bottom of the "less than" or "greater than" symbol like this:

The "less than or equal to" sign:		≤
The "greater than or equal to" sign:		≥

All The Symbols

Here is a summary of all the symbols:

Symbol	Words	Example Use
=	equals	1 + 1 = 2
≠	not equal to	1 + 1 ≠ 1
>	greater than	5 > 2
<	less than	7 < 9
≥	greater than or equal to	marbles ≥ 1
≤	less than or equal to	dogs ≤ 3

Why Use Them?

Because there are things we do not know exactly ...

... but can still say something about.

So we have ways of saying what we do know (which may be useful!)

Example: John had 10 marbles, but lost some. How many has he now?

Answer: He must have less than 10:

Marbles < 10

If John still has some marbles we can also say he has greater than zero marbles:

Marbles > 0

But if we thought John could have lost all his marbles we would say

Marbles ≥ 0

In other words, the number of marbles is greater than or equal to zero.

Combining

We can sometimes say two (or more) things on the one line:

Example: Becky starts with $10, buys something and says "I got change, too". How much did she spend?

Answer: Something greater than $0 and less than $10 (but NOT $0 or $10):

"What Becky Spends" > $0
"What Becky Spends" < $10

This can be written down in just one line:

$0 < "What Becky Spends" < $10

That says that $0 is less than "What Becky Spends" (in other words "What Becky Spends" is greater than "$0") and what Becky Spends is also less than $10.

Notice that ">" was flipped over to "<" when we put it before what Becky spends - always make sure the small end points to the small value.

Changing Sides

We saw in that previous example that when we change sides we flipped the symbol as well.

This:		Becky Spends > $0	(Becky spends greater than $0)
is the same as this:		$0 < Becky Spends	($0 is less than what Becky spends)

Just make sure the small end points to the small value!

Here is another example using "≥" and "≤":

Example: Becky has $10 and she is going shopping. How much will shespend (without using credit)?

Answer: Something greater than, or possibly equal to, $0 and less than, or possibly equal to, $10:

Becky Spends ≥ $0
Becky Spends ≤ $10

This can be written down in just one line:

$0 ≤ Becky Spends ≤ $10

A Long Example: Cutting Rope

Here is an interesting example I thought of:

Example: Sam cuts a 10m rope into two. How long is the longer piece? How long is the shorter piece?

Answer: Let us call the longer length of rope "L", and the shorter length "S"

L must be greater than 0m (otherwise it isn't a piece of rope), and also less than 10m:

L > 0
L < 10

So:

0 < L < 10

That says that L (the Longer length of rope) is between 0 and 10 (but not 0 or 10)

The same thing can be said about the shorter length "S":

0 < S < 10

But I did say there was a "shorter" and "longer" length, so we also know:

S < L

(Do you see how neat mathematics is? Instead of saying "the shorter length is less than the longer length", we can just write "S < L")

We can combine all of that like this:

0 < S < L < 10

That says a lot:

0 is less that the short length, the short length is less than the long length, the long length is less than 10.

Reading "backwards" we can also see:

10 is greater than the long length, the long length is greater than the short length, the short length is greater than 0.

It also lets us see that "S" is less than 10 (by "jumping over" the "L"), and even that 0<10 (which we know anyway), all in one statement.

NOW, I have one more trick. If Sam tried really hard he might be able to cut the rope EXACTLY in half, so each half is 5m, but we know he didn't because we said there was a "shorter" and "longer" length, so we also know:

S<5

and

L>5

We can put that into our very neat statement here:

0 < S < 5 < L < 10

And IF we thought the two lengths MIGHT be exactly 5 we could change that to

0 < S ≤ 5 ≤ L < 10

An Example Using Algebra

OK, this example may be complicated if you don't know Algebra, but I thought you might like to see it anyway:

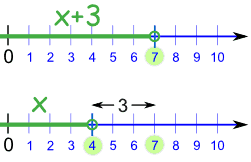
Example: What is x+3, when we know that x is greater than 11?

If x > 11 , then x+3 > 14

(Imagine that "x" is the number of people at your party. If there are more than 11 people at your party, and 3 more arrive, then there must be more than 14 people at your party now.)